Я не буду приводить никаких технических характеристик этих устройств: я рассчитываю на то, что вы уже ознакомились с их строением и жаждете применить их.

Данное градуирование построено, грубо говоря, на двух шагах.

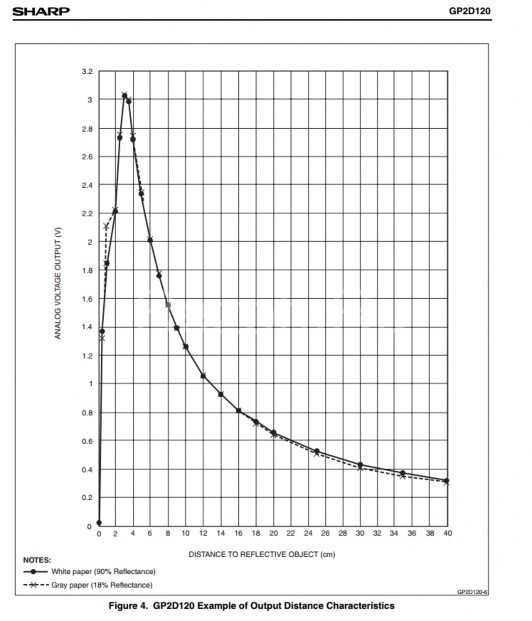
Используем график зависимости выдаваемого напряжения от расстояния, идущий в сопровождающей документации к вашему датчику.
Мысленно разобьем этот нелинейный график на множество линейных отрезков (как бы интерполируем). Первое, что нужно сделать – это аккуратно, следуя по графику, выписать все отмеченные точки в виде (вольтаж ; дистанция). Выписывайте только те точки, что находятся в зоне видимости – эти точки лежат на чём-то похожем на гиперболу.

Наш график из документации

Теперь создаем два массива чисел с плавающими точками и в первый заносим вольтаж ( по убыванию), а во второй – соответствующие расстояния. Вот так получилось у меня для дальнометра Sharp GP2D120X (4 – 40 см):

float voltage[] = {
2.7, 2.34, 2.00, 1.78,
1.56, 1.4, 1.265, 1.06,
0.92, 0.8, 0.74, 0.66,
0.52, 0.42, 0.36, 0.32};
 
float distanse[] = {
4.0, 5.0, 6.0, 7.0,
8.0, 9.0, 10.0, 12.0,
14.0, 16.0, 18.0, 20.0,
25.0, 30.0, 35.0, 40.0};

Итак, мы должны получить входную данную и сравнить её с массивом вольтажа. Для этого переводим безразмерное число в вольты умножением показания датчика на коэффициент 0.004882812 (это 5 / 1024 ):

int inc = analogRead(SenPin);
float volt_read = float(inc) * 0.004882812;

Если же вы заинтересованны в хорошем результате, то я не рекомендую записывать этот кусок прямо так. Вы ведь, наверное, не раз сталкивались с тем, что иногда показания датчика «скачут». С этим надо бороться: добавляем строчку, которая будет несколько раз с минимальной задержкой опрашивать датчик и выводить средний результат. Уверяю вас, это повлияет на точность в лучшую сторону!

//здесь kk – количество замеров, а r – переменная для записи показаний (безразмерная)

int kk = 12, r;
for(int i = 1; i < kk; i++)
{
    r = r + analogRead(SenPin);
    delay(8);
}
r = r / kk;

Теперь, когда есть достаточно точное показание датчика, перейдём к основной части этого шага – к нахождению в массиве вольтажа самого ближнего значения. Я сделал это методом последовательного перебора, хотя вы можете с легкостью решить эту задачу и методом половинного деления.

float volt_read = float(r) * 0.004882812;
if((voltage[i] > volt_read) && (voltage[N] < volt_read))
{
    for (i; i < N; i++) { if(volt_read >= voltage[i+1])
    {
        n1 = i;
        i = N;
    }
}

В моём примере вводимое число сначала проверяется на принадлежность к заданному числовому ряду, что, конечно, необязательно, так как с графика списывались только «надёжные» точки ( не хочется, чтобы код зависал из-за фигни). Далее идет поиск перебором, где n1 = i; — то число, которого вводимое больше. А i = N; выполняется для того, чтобы сразу закончить поиск.

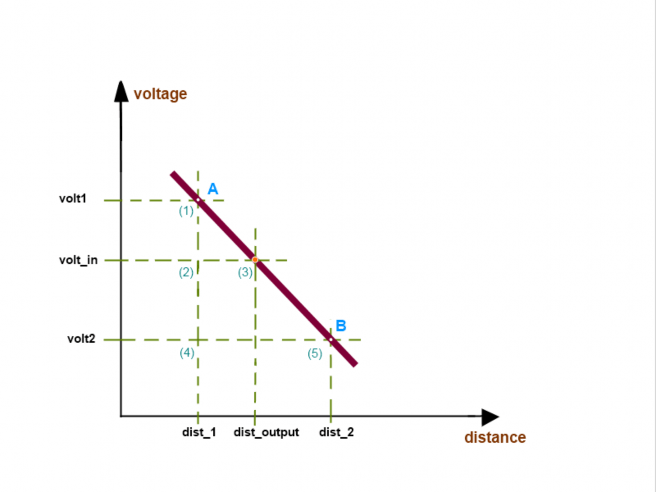
Теперь второй шаг. Он бесконечно прост и красив. В нём всё опирается на геометрию седьмого класса. У нас достаточно входных данных: промежуток точек, в котором находится наш вольтаж; расстояние, соответствующее вольтажу; и наш входной вольтаж.
Если говорить в общем виде, то у нас имеются два подобных прямоугольных треугольника (1-4-5 и 1-2-3), в которых всё известно, кроме выходного расстояния (dist_output) – смотрите график.

Сравниваем подобные треугольники и находим расстояние до предмета:

float x1, x2, y1, y2, y_in;
y1 = voltage[n1];
x1 = distanse[n1];
y2 = voltage[n1 + 1];
x2 = distanse[n1 + 1];
y_in = volt_read;
 
dist = (x2 - x1)*(y1 - y_in)/(y1 - y2) + x1;

Вот фотографии для лучшего усвоения материала:

Вот единая функция, включающая всё описанное в статье

float get_dist(int SenPin)
{
// замеренные константы справедливы только для Sharp GP2D120X
const float voltage[] = {
2.7, 2.34, 2.00, 1.78,
1.56, 1.4, 1.265, 1.06,
0.92, 0.8, 0.74, 0.66,
0.52, 0.42, 0.36, 0.32 };
 
const float distance[] = {
4.0, 5.0, 6.0, 7.0,
8.0, 9.0, 10.0, 12.0,
14.0, 16.0, 18.0, 20.0,
25.0, 30.0, 35.0, 40.0};
 
int kk = 12, r, n1, i = 0, N = 15;
for(int i = 1; i < kk; i++)
{
    r = r + analogRead(SenPin);
    delay(8);
}
r = r / kk;
 
float volt_read = float(r) * 0.004882812;
    if((voltage[i] > volt_read) && (voltage[N] < volt_read))
    {
        for (i; i < N; i++)
        {
            if(volt_read >= voltage[i+1])
                {
                     n1 = i;
                     i = N;
                }
        }
        float y1 = voltage[n1];
        float x1 = distance[n1];
        float y2 = voltage[n1 + 1];
        float x2 = distance[n1 + 1];
        float y_in = volt_read;
        float distance_out = (x2 - x1)*(y1 - y_in)/(y1 - y2) + x1;
        return distance_out;
    }
}